Hvor mye over- eller underrepresenterer egentlig d’Hondts metode? La oss vende tilbake til eksempelet over og prøve å illustrere det med et kakediagram:
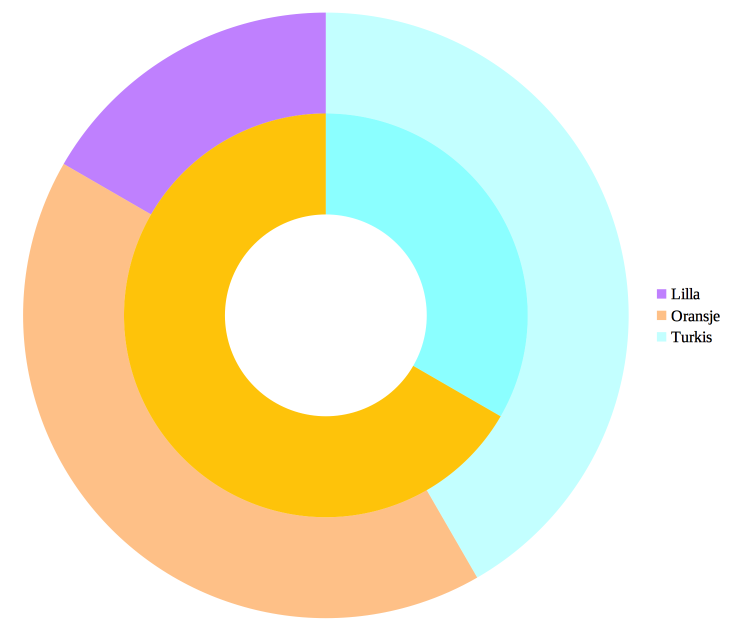 Vi ser at Oransje sluker hele Lilla og deler av Turkis. Dette var ikke akseptabelt for en franskmann ved navn Sainte-Laguë, som kom opp med en annen idé.
Vi ser at Oransje sluker hele Lilla og deler av Turkis. Dette var ikke akseptabelt for en franskmann ved navn Sainte-Laguë, som kom opp med en annen idé.
Vi bruker serien 1, 2, 3 … som divisorer. Hvordan ville det sett ut hvis vi brukte, la oss si, 1, 3, 5 …? La oss gå tilbake til tabellen:
| Mandat | |||
|---|---|---|---|
| 1. | 2. | 3. | |
| Oransje | 150 015 | 50 005 | 30 003 |
| Turkis | 150 000 | 50 000 | 30 000 |
| Lilla | 60 000 | 20 000 | 12 000 |
Vi ser at fordelingen er mindre skjev til fordel for de store partiene. Grafisk fremstilt ser det slik ut: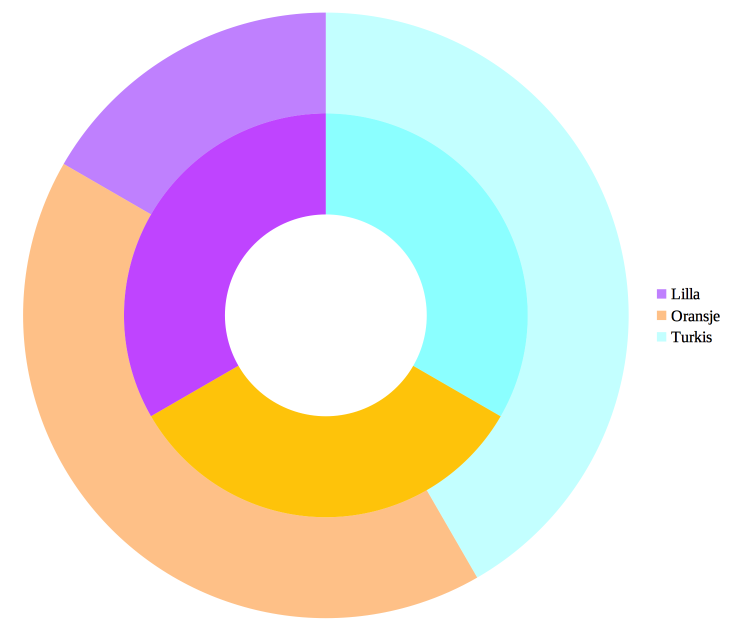 Hvor kommer serien 1, 3, 5 … fra? Dessverre bare fra Pierre Sainte-Laguës fantasi. Den kunne vært 1, 5, 9 …, 1, 4, 8 … eller til og med 42, 15, 3,14 …, og man kunne konstruert en metode rundt den. Dog er det, fordi vi snakker om multipla, tilfelle at ethvert valg av serier som kan skrives på felles faktor med en annen, vil være ekvivalent. 2, 4, 6 … vil derfor være ekvivalent med 1, 2, 3 … fordi \(2, 4, 6 … = 2\cdot(1, 2, 3 …)\).
Hvor kommer serien 1, 3, 5 … fra? Dessverre bare fra Pierre Sainte-Laguës fantasi. Den kunne vært 1, 5, 9 …, 1, 4, 8 … eller til og med 42, 15, 3,14 …, og man kunne konstruert en metode rundt den. Dog er det, fordi vi snakker om multipla, tilfelle at ethvert valg av serier som kan skrives på felles faktor med en annen, vil være ekvivalent. 2, 4, 6 … vil derfor være ekvivalent med 1, 2, 3 … fordi \(2, 4, 6 … = 2\cdot(1, 2, 3 …)\).
Men som vi vil se: hvis en nederlender kan finne opp en idé og en franskmann forvanske den, finnes det alltids en skandinav som kan rote den helt til.